I thought it would be cool to write a hill climbing algorithm that replicates images by drawing random circles.
A hill climbing algorithm proceeds toward a goal through a trial and error process. At each iteration, the algorithm makes a small, random change to its current solution. If the change brings the algorithm closer to its goal, the change is kept. Otherwise the algorithm discards the change and tries again.
In this project, the small random changes are random circles which the algorithm draws on its generated image. If a random circle makes the generated image more similar to the target image its kept as part of the solution. Otherwise the circle is discarded and the algorithm tries a different random circle. After enough random circles the algorithm should generate an image that is reminiscent of the given target image but hopefully with a nice random, artistic quality.
Code
A Jupyter Notebook is available on my GitHub or just copy and paste code from this post.
Pip install required packages:
python -m pip install --upgrade Pillow
python -m pip install --upgrade matplotlib
Python imports:
import random
import numpy as np
from time import perf_counter
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw, ImageChops
Images with the Pillow library
For this post I’ll be using this image of Jimi Hendrix as the target image which the algorithm will replicate. I’m using the Pillow library which is useful for manipulating and generating images in Python.
# open the target image
target_image_path = 'images/Jimi_Hendrix_1967_uncropped.jpg'
im_target = Image.open(target_image_path).convert('L')
im_target

While the original image looks like it’s already in grayscale, the .convert('L') method ensures that the image object uses Pillow’s luminance or grayscale mode.
We can work with the PIL.Image object but can also convert to a numpy array.
Because I’m working in grayscale mode, the numpy array of this image is simply a 2d array where each pixel is represented by a number (dtype=np.uint8) between 0, representing black, and 255, representing white.
# the pixels of the image as an array
np.asarray(im_target)
array([[153, 133, 133, ..., 187, 196, 187],
[155, 152, 137, ..., 190, 195, 188],
[160, 158, 155, ..., 190, 193, 173],
...,
[233, 243, 244, ..., 157, 140, 120],
[235, 237, 237, ..., 157, 112, 109],
[233, 235, 235, ..., 143, 94, 88]], dtype=uint8)
print(np.asarray(im_target).shape)
print(np.asarray(im_target).T.shape == im_target.size)
(954, 1280)
True
The dimensions of the numpy array match those of the target image.
Note that Image.size has the horizontal dimension as the 0th element followed by the vertical dimension which is why I transform (.T) the numpy array when checking for equality of dimensions.
Also note that Pillow image coordinates start with (0, 0) in the upper left corner.
Drawing Circles
I use Pillow’s ImageDraw module for drawing circles.
# image with a black circle
im1 = Image.new(mode='L', size=(100, 100), color=255)
draw = ImageDraw.Draw(im1)
draw.ellipse(xy=((25, 0), # starting coordinate
(75, 50)), # ending coordinate
fill=0)
im1

This code initiates a new image object, im1, that’s 100 by 100 pixels, in grayscale mode, with a white background.
The draw object modifies the im1 object in place and the xy parameter defines the bounding box of the ellipse.
Image comparison
The hill climbing algorithm needs a way to compare images so it can tell whether a random circle makes its generated image look more like the target image. Naturally, different ways of comparing images will affect how the algorithm converges toward the target image. This choice will change the look of the resulting image and potentially how many iterations the algorithm takes before it starts to look like the target.
I’ll use the following method to measure the difference between images:
- For each pixel in the generated image, find the absolute difference in luminescence between that pixel and the corresponding pixel in the target image.
I.e. if a particular generated pixel is white (255) and the corresponding target pixel is gray (125) the difference would be
abs(255 - 125) = 130. - Do this for all pixels in the image.
- Average the difference of all pixels and standardize the result to [0, 1].
When many of the pixels are similar, the overall average differences will be small, and the difference measure will be close to 0. With this method the difference between an image and its negative will be 1, while on average the difference between any two unrelated images will likely be close to 0.5.
Pillow’s ImageChops.difference function performs steps 1 and 2 and returns the result.
# image to compare with im1
im2 = Image.new(mode='L', size=(100, 100), color=255)
draw = ImageDraw.Draw(im2)
draw.ellipse(xy=((50, 0), # starting coordinate
(100, 50)), # ending coordinate
fill=180)
im2

What’s the difference between im1 from above and im2?
im_diff = ImageChops.difference(im1, im2)
im_diff

The images have the same white background which shows as black in the difference image (difference = 0).
The black circle in im1 is completely different from the white background of im2 and shows up as a white crescent (difference = 255).
The gray circle in im2 is an in between gray relative to the black circle and the white background of im1.
I apply step 3 and find the average difference of all pixels in the difference image and standardize to between 0 and 1.
array_diff = np.asarray(im_diff)
percent_diff = array_diff.mean() / 255 # standardize to percent terms
print(f'im1 and im2 are {round(percent_diff * 100, 2)}% different')
im1 and im2 are 21.44% different
Putting all this in a function:
def find_img_diff_pct(im1: Image.Image, im2: Image.Image) -> float:
assert im1.size == im2.size
return np.asarray(ImageChops.difference(im1, im2)).mean() / 255
Drawing random circles
Similar to the choice of method for image comparison, the choice of how the algorithm makes random changes will affect convergence and the look of the generated image. I’d like to add some constraints to the random changes which will help the algorithm converge without sacrificing too much of the unpredictability which will make the generated image interesting.
Take, for example, circle size. Intuitively it makes sense that the circle size should decrease as the generated image becomes more complete. As the hill climbing algorithm progresses, the differences between the generated and target images will be found mostly in the fine details. Filling in these details will require progressively smaller circles. Imagine how inefficient it would be if, many iterations in and with a moderately detailed generated image, the algorithm randomly drew a very large circle in the middle of the generated image.
Rather than simply using a linear decrease in circle size, I’d like the algorithm to spend more time with smaller circles. Smaller circles are more difficult to randomly place in the correct spot. To flush out some of the fine detail in the target image the algorithm will need more tries to place small circles in the right place. Furthermore, a greater number of small circles is required to fill in this detail whereas only a few well placed large circles are needed to appropriately match the target image background.
After experimenting a bit I decided to use a modified logarithmic function to interpolate between a starting and ending circle radius.
The choose_circle_radius function takes a float in [0, 1] representing the percentage of iterations completed and returns a circle radius, with some random variability.
The alpha_func function takes the percentage of iterations complete, maps it to a logarithmic function, and returns a value in [0, 1] which I use to lerp between CIRCLE_START_RADIUS and CIRCLE_END_RADIUS.
I add variability to the circle radius with the CIRCLE_PERCENT_VARIANCE parameter.
CIRCLE_START_RADIUS = 100
CIRCLE_END_RADIUS = 4
CIRCLE_PERCENT_VARIANCE = 0.2
def choose_circle_radius(percent_complete: float) -> float:
alpha = alpha_func(percent_complete)
circle_radius_target = int(CIRCLE_START_RADIUS -
(CIRCLE_START_RADIUS - CIRCLE_END_RADIUS)
* alpha
)
# add a bit of variance to the circle radius
circle_radius = int(random.uniform(1 - CIRCLE_PERCENT_VARIANCE,
1 + CIRCLE_PERCENT_VARIANCE)
* circle_radius_target)
return circle_radius
def alpha_func(x: float) -> float:
"""x in range [0, 1] returns range [0, 1]"""
assert 0 <= x <= 1
# return x # linear
return loglike(x)
def loglike(x: float, stretch: int = 40) -> float:
return np.log((x * stretch) + 1) / np.log(stretch + 1)
Here’s an example of how the circle radius will decrease as iterations increase.
x = np.linspace(0, 1)
y = [choose_circle_radius(_x) for _x in x]
plt.plot(x, y)
plt.xlabel('percent_complete')
plt.ylabel('random circle radius')
plt.show()
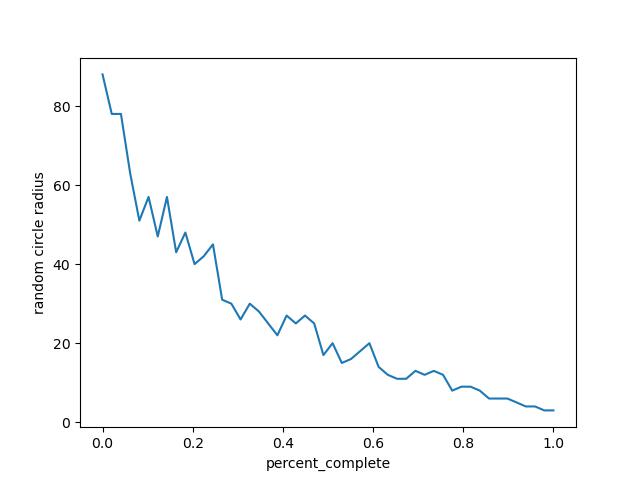
You can see how the radius starts at 100 pixels but quickly decreases and spends around half of the iterations below 20 pixels.
Complete script
As a reminder, the hill climbing algorithm follows these steps for each iteration:
- Measure the difference between the generated image and target image.
- Draw a random circle on the generated image.
- Measure the difference between this new generated image and the target.
- Is the new image with the random circle more similar to the target?
- If so, keep the circle!
- Otherwise, discard it.
- Rinse and repeat…
Here’s the full code.
import random
import numpy as np
from time import perf_counter
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw, ImageChops
BLACK = 0
WHITE = 255
CIRCLE_START_RADIUS = 100
CIRCLE_END_RADIUS = 4
CIRCLE_PERCENT_VARIANCE = 0.2
MAX_ITERATIONS = 100_000
# for reproducibility
SEED = 1111
random.seed(SEED)
np.random.seed(SEED)
def find_img_diff_pct(im1: Image.Image, im2: Image.Image) -> float:
assert im1.size == im2.size
return np.asarray(ImageChops.difference(im1, im2)).mean() / 255
def choose_circle_radius(percent_complete: float) -> float:
alpha = alpha_func(percent_complete)
circle_radius_target = int(CIRCLE_START_RADIUS -
(CIRCLE_START_RADIUS - CIRCLE_END_RADIUS)
* alpha
)
# add a bit of variance to the circle radius
circle_radius = int(random.uniform(1 - CIRCLE_PERCENT_VARIANCE,
1 + CIRCLE_PERCENT_VARIANCE)
* circle_radius_target)
return circle_radius
def alpha_func(x: float) -> float:
"""x in range [0, 1] returns range [0, 1]"""
assert 0 <= x <= 1
# return x # linear: for x in [0, 1] just returns x
return loglike(x)
def loglike(x: float, stretch: int = 40) -> float:
return np.log((x * stretch) + 1) / np.log(stretch + 1)
# open the target image
target_image_path = 'images/Jimi_Hendrix_1967_uncropped.jpg'
im_target = Image.open(target_image_path).convert('L')
np_target = np.array(im_target)
X_MAX = im_target.size[0]
Y_MAX = im_target.size[1]
# initial blank starting image
im_generated = Image.new(mode='L', size=im_target.size, color=WHITE)
# 1 initial difference
diff_generated_init = find_img_diff_pct(im_generated, im_target)
diff_generated = diff_generated_init
diff_compare = diff_generated
num_pixels = np.ones(im_target.size).size
# keep track of progress
diff_list = []
guess_diff_list = []
good_guess_pct_list = []
good_guesses = 0
epoch = 0
# time progress
t0 = perf_counter()
while epoch < MAX_ITERATIONS:
# random radius
circle_radius = choose_circle_radius(epoch / MAX_ITERATIONS)
# random center point
circle_center_x = random.randrange(0, X_MAX)
circle_center_y = random.randrange(0, Y_MAX)
# start/end points as (x, y)
circle_start_point = (circle_center_x - circle_radius,
circle_center_y - circle_radius)
circle_stop_point = (circle_center_x + circle_radius,
circle_center_y + circle_radius)
# random color
circle_color = random.randrange(BLACK, WHITE+1, 1)
# copy current working image
im_compare = ImageChops.duplicate(im_generated)
# draw a random shape on it
draw = ImageDraw.Draw(im_compare)
draw.ellipse((circle_start_point, circle_stop_point),
fill=circle_color)
# find difference of new im_compare with target
diff_compare = find_img_diff_pct(im_target, im_compare)
# if new image is less different than previous generated im
if diff_compare < diff_generated:
# switch working image to the new im_compare
im_generated = ImageChops.duplicate(im_compare)
diff_generated = diff_compare
good_guesses += 1
# else just keep the working image without the random shape
# print progress
if epoch % 10_000 == 0:
# if epoch % 2500 == 0:
print(f'epoch: {epoch}, difference: {diff_generated}')
epoch += 1
diff_list.append(diff_generated)
guess_diff_list.append(diff_compare)
good_guess_pct_list.append(good_guesses / epoch)
t1 = perf_counter()
print(f'epoch: {epoch}, difference: {diff_generated}')
print(f'number of good guesses: {good_guesses}')
print(f'good guess percent: {good_guesses / epoch}')
print(f'Total time: {round((t1 - t0) / 60, 2)} min')
# combine generated, difference, and target images for easier viewing
im_diff = ImageChops.difference(im_target, im_generated)
new_size = (int(im_target.size[0]/3), int(im_target.size[1]/3))
im_display = Image.new('L', (im_target.size[0], new_size[1]), 255)
im_display.paste(im_generated.resize(new_size), (0, 0))
im_display.paste(im_diff.resize(new_size), (new_size[0], 0))
im_display.paste(im_target.resize(new_size), (new_size[0]*2, 0))
im_display
epoch: 0, difference: 0.3492539346713528
epoch: 10000, difference: 0.11385856635631192
epoch: 20000, difference: 0.10548068054527891
epoch: 30000, difference: 0.0974889815071731
epoch: 40000, difference: 0.09126970547128704
epoch: 50000, difference: 0.08784024052493114
epoch: 60000, difference: 0.0839930876700785
epoch: 70000, difference: 0.080742144145394
epoch: 80000, difference: 0.07778092821247996
epoch: 90000, difference: 0.07505323945615983
epoch: 100000, difference: 0.07270399787273399
number of good guesses: 3940
good guess percent: 0.0394
Total time: 6.09 min

Left to right - the final generated, difference, and target images.
And the final result!
im_generated

Overall I’m really pleased with the result. At a glance it’s pretty clearly Jimi playing his guitar but when you try to focus on any details they just become a mess of circles. I especially like how the headstock on the guitar is just a handful of black and gray circles against the light background and how the curly top righ part of Jimi’s hair was generated.
The final difference with the target image is 7.3%. Although the script tries 100,000 random circles only 3,940 of them improve the generated image and are included in the final result. 3.94% seems pretty inefficient although I haven’t experimented to see how much better it could get. Altering the random circle generation method could improve this.
Here’s a plot of the difference between generated and target images at each iteration. I also plot the percent of circle guesses up to that point which have improved the generated image - i.e. correct guesses.
# plot progress stats
x = np.arange(MAX_ITERATIONS)
fig, ax = plt.subplots()
ax.plot(x, good_guess_pct_list, label='correct guess %')
ax.plot(x, guess_diff_list, label='guess difference')
ax.set_yscale('log')
ax.set_xlabel('Epoch')
fig.legend()
plt.show()
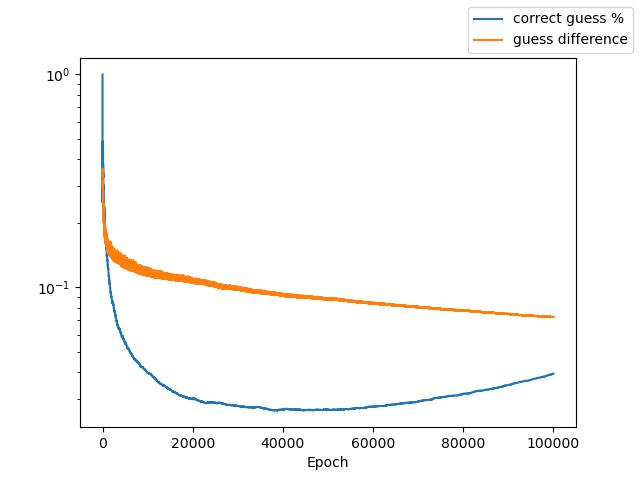
I find it interesting that the frequency of correct guesses actually starts increasing around half way through. I’ve noticed this pattern across a bunch of different iterations of this project but don’t have a good sense why it happens. Maybe once the circles reach a certain, small size they start improving the similarity to the target image simply because they match some of the natural graininess of the photo. If you have thoughts shoot me an email.
Conclusion
This is just one, simple application of hill climbing to generate art. You could apply this technique in many other ways or combine with other methods as part of a larger generative art piece.
Some variations could include:
- Different shapes or a combination of shapes.
- Adding color: You could choose color completely randomly or use the background image to determine the color of shapes. You could even use a color format like hsl, set the hue and saturation, and just randomly choose the luminescence.
- I tried altering the random placement of the circles by making them more likely to appear in areas of the image where the difference was greatest. This took a lot longer (although my implementation was probably inefficient) and didn’t produce results that were that much better. But maybe there’s more that could be done along these lines.
If you’re aware of any cool uses of hill climbing algorithms in generative art I’d be interested to see them. Or if you have thoughts, questions, or critiques, shoot me an email at hello at abrefeld.anonaddy.com.